REOI Round #1
下发文件:
| 题目名称 | 春日窃贼 | 靛蓝二次方 | 仅予你的晴天 | 所以我放弃了音乐 |
|---|---|---|---|---|
| 题目类型 | 传统型 | 传统型 | 传统型 | 传统型 |
| 可执行文件名 | spring |
square |
sunny |
starry |
| 输入文件 | spring.in |
square.in |
sunny.in |
starry.in |
| 输出文件 | spring.out |
square.out |
sunny.out |
starry.out |
| 时间限制 | ||||
| 空间限制 | ||||
| 评测方式 | 逐测试点 | 逐测试点 | 子任务捆绑 | 逐测试点 |
| 比较方式 | 自定义校验器 | 全文比较 | 全文比较 | 全文比较 |
T1 春日窃贼 (spring)
题目背景
落花纷纷 我们连呼吸都忘却
连眨眼都觉得麻烦
今日春色 明日回忆
只是等待着一阵风
题目描述
具体来说,春日时光可以被分割成 条 首尾相接 的线段 。每条线段的每个端点都是整数。 保证第一条线段的左端点为 且最后一条线段的右端点为 。
你,为了盗走这美妙的春日,也精心构造了 条首尾相接的线段 ,同样每条线段的每个端点都必须是整数,并且你得保证第一条线段的左端点为 且最后一条线段的右端点为 。
你得到的春天长度以如下方式计算:
-
对于每个 ,取春天的第 条线段和你构造的第 条线段交集之长度,记为 ,例如线段 和线段 的交集长度为 。
-
你得到的长度即为 ,即这些交集长度之总和。
春天就快要结束了,你已经得到了所有的 ,现在请你构造出你的 ,使得你得到的春天长度恰好为 。
输入格式
本题包含多组测试数据。
第一行包含两个整数 ,表示测试点的编号和测试数据的组数。在样例中, 表示该样例与测试点 的数据范围相同。
接下来包含 组数据,每组数据的格式如下:
-
第一行三个整数 。
-
第二行一个长度为 的整数序列 ,表示这些线段的分割点。具体地, 。
-
保证 。
输出格式
对于每组数据,输出一行,格式如下:
要是你无论如何也不可能盗取长度为 的春天,输出一个整数 即可。
否则的话,你需要输出一个长度为 的整数序列 ,表示你构造的方案。具体地,,中间用空格隔开。
并且你要保证 。
如果有多种方案,输出任意一种即可。
样例 #1
样例输入 #1
1 3 |
样例输出 #1
0 1 2 6 10 |
提示
【样例 1 解释】
对于第一组数据:
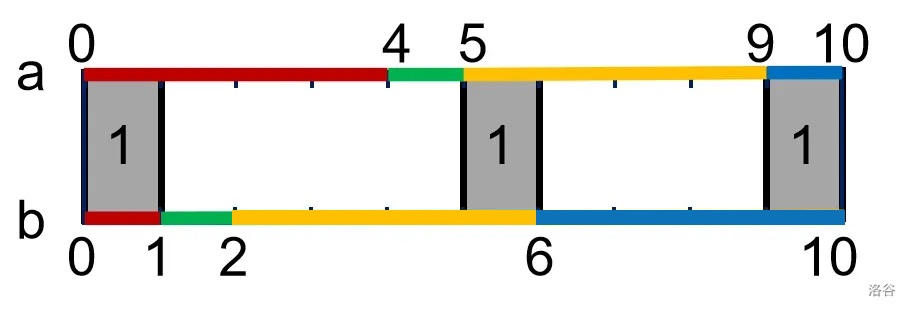
其中线段 表示原来的春日时光,线段 表示样例构造的方案,灰色部分表示交集,你得到的春日长度为 。
对于第二组数据:
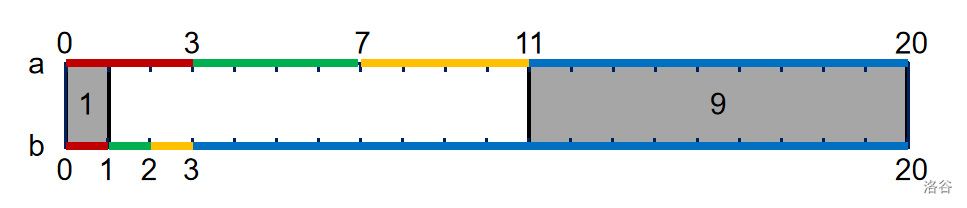
其中线段 表示原来的春日时光,线段 表示样例构造的方案,灰色部分表示交集,你得到的春日长度为 。
对于第三组数据,可以证明不存在合法的方案。
【样例 2】
见下发文件中的 spring/spring2.in 与 spring/spring2.ans。
该样例满足测试点 。
【样例 3】
见下发文件中的 spring/spring3.in 与 spring/spring3.ans。
该样例满足测试点 。
【样例 4】
见下发文件中的 spring/spring4.in 与 spring/spring4.ans。
该样例满足测试点 。
【样例 5】
见下发文件中的 spring/spring5.in 与 spring/spring5.ans。
该样例满足测试点 。
【样例 6】
见下发文件中的 spring/spring6.in 与 spring/spring6.ans。
该样例满足测试点 。
【样例 7】
见下发文件中的 spring/spring7.in 与 spring/spring7.ans。
该样例满足测试点 。
【数据范围】
| 测试点编号 | ||
|---|---|---|
对于全部数据,,,,,,。
由于题目原因,样例输出中仅有 Yes 或 No 表示该测试点是否有解。
我们在附件中提供了 checker.cpp 供你在本地验证自己输出的正确性。
你需要在 C++14 环境下编译它,并将它与你的输入输出文件(要求命名为 spring.in spring.out) 放在同一目录下运行。
T2 靛蓝二次方 (square)
题目背景
无尽的晴空映入流泪的眼眶,泪水和瞳孔映出两重蓝天。
远处的白云上似有花瓣浮游,这令人目眩的靛蓝二次方。
题目描述
有一个 的 01 矩阵,每格 0 代表蓝天,1 代表白云。每次操作,你可以选择将一行或是一列上的蓝天变成白云,白云变成蓝天(如果原本是 0,就变成 1;如果原本是 1,就变成 0)。
请你计算通过有限次操作,最多能够有多少格白云,满足它所在的行和列都有且仅有它一朵白云(即该点所在的行和列都只有该点是 1)。
输入格式
本题包含多组测试数据。
第一行两个整数 ,表示测试点的编号和测试数据的组数。在样例中, 表示该样例与测试点 的数据范围相同。
接下来包含 组数据,每组数据的格式如下:
-
第一行两个整数 。
-
接下来 行,每行一个长为 的字符串,表示天空。
输出格式
对于每组测试数据输出一行,包含一个整数,表示对应的答案。
样例 #1
样例输入 #1
1 2 |
样例输出 #1
1 |
提示
【样例 1 解释】
对于第一组数据,可以对第 行和第 列操作,此时的天空变为
110 |
只有第 行第 列的白云满足条件。第 行的两块白云不满足条件,因为同一行还有其它白云。可以证明无法使更多的白云同时满足条件。
对于第二组数据,可以对第 行和第 列进行操作,此时的天空变为:
010 |
其中三块白云都满足条件。
【样例 2】
见下发文件中的 square/square2.in 与 square/square2.ans。
该样例满足测试点 。
【样例 3】
见下发文件中的 square/square3.in 与 square/square3.ans。
该样例满足测试点 。
【样例 4】
见下发文件中的 square/square4.in 与 square/square4.ans。
该样例满足测试点 。
【样例 5】
见下发文件中的 square/square5.in 与 square/square5.ans。
该样例满足测试点 。
【样例 6】
见下发文件中的 square/square6.in 与 square/square6.ans。
该样例满足测试点 。
【数据范围】
| 测试点编号 | 特殊性质 | ||
|---|---|---|---|
| 无 | |||
| 有 | |||
| 无 | |||
| 无 | |||
| 无 |
- 特殊性质:保证矩阵里要么全是蓝天,要么全是白云。
对于全部数据,,,。
T3 仅予你的晴天 (sunny)
题目背景
就这样不知不觉成为了大人
我说不出口 而仅予你以晴天
题目描述
Elma 在房间的一个角落中找到了一个有 个元素的整数序列。她觉得这个数列不好看,于是她决定把这个序列变漂亮一点。
具体来说,她会对数列进行以下操作:
-
在数列的尾部加入一个值为 的数。
-
删除数列一个长度为 的后缀。
-
在序列的开头加入一个值为 的数。
-
删除数列一个长度为 的前缀。
同时,为了保证自己的序列在变漂亮,她会问你一些问题:
- 区间 中有多少个数大于等于 且小于等于 ?
输入格式
第一行包含一个整数 ,表示该测试点所属的子任务的编号。在样例中, 表示该样例与测试点 的数据范围相同。
第二行个整数 。
第三行 个整数 ,表示初始的数列。
第四行到第 行,每行表示一个操作:
-
1 x表示在数列的尾部加入一个值为 的数 -
2 k表示删除数列的长度为 的后缀。 -
3 x表示在数列的开头加入一个值为 的数。 -
4 k表示删除数列的长度为 的前缀。 -
5 l r x y表示询问区间 中有多少个数大于等于 且小于等于 。
输出格式
对于每次操作 5,输出一行一个整数,表示答案。
样例 #1
样例输入 #1
1 |
样例输出 #1
1 |
提示
【样例 1 解释】
下表展示了每一次操作后的数列。
| 操作编号 | 序列 | 操作 |
|---|---|---|
| / | ||
1 1 |
||
3 4 |
||
5 1 3 2 3 |
||
4 2 |
||
1 1 |
||
5 1 4 4 1 |
【样例 2】
见下发文件中的 sunny/sunny2.in 与 sunny/sunny2.ans。
该样例满足测试点 。
【样例 3】
见下发文件中的 sunny/sunny3.in 与 sunny/sunny3.ans。
该样例满足测试点 。
【样例 4】
见下发文件中的 sunny/sunny4.in 与 sunny/sunny4.ans。
该样例满足测试点 。
【样例 5】
见下发文件中的 sunny/sunny5.in 与 sunny/sunny5.ans。
该样例满足测试点 。
【样例 6】
见下发文件中的 sunny/sunny6.in 与 sunny/sunny6.ans。
该样例满足测试点 。
【样例 7】
见下发文件中的 sunny/sunny7.in 与 sunny/sunny7.ans。
该样例满足测试点 。
【数据范围】
本题开启子任务捆绑测试。
记 为当前数列的长度。
对于全部数据,保证 ,,,,。
子任务 1(4 分):。
子任务 2(8 分):。
子任务 3(12 分):保证仅存在操作 。
子任务 4(16 分):保证不存在操作 和操作 。
子任务 5(20 分):保证不存在操作 和操作 。
子任务 6(40 分):无特殊限制。
T4 所以我放弃了音乐 (starry)
题目背景
这样全都搞错了啊 已经够了 你们这些人啊
爱啊感情啊人生啊梦想啊 全都无所谓了
正确的答案迟迟说不出口只是防卫本能啊
思虑良久 都是你的错啊
题目描述
Elma 在那张废弃的乐谱上无谓地乱涂乱画着。
乐谱用一个长度为 的正整数序列 表示。序列中的每个元素代表一个音符,这个元素的值代表它的音高 。
具体地说,每次涂改会随机交换两个音符的位置 ,即于 这 个位置对中随机选择一个位置对 ,并将 和 交换。
虽然乐谱已经废弃,谱曲的那个人也已经不在了,但是她依然期待着在 次涂改后,这些音符会奇迹般地排列成另外一段美妙的旋律。
我们定义一对数 是“不和谐对”,如果 且 ,形象地说,就是两个距离 小于等于 的音符,跨度却 大于等于 了 。乐谱的“不和谐度”为其中不和谐对的个数。
经过 次涂改,最终的序列有 中情况。尽管在一些情况中最终生成的序列本质相同,但是我们仍然将其视作两种情况,也就是说 两个情况不同,当且仅当至少在一次涂改中,两个情况里交换的位置对不同 。
现在她想知道经过 次涂改,最终所有情况中乐谱的不和谐度之和。
答案对 取模。
输入格式
第一行一个整数 ,表示测试点的编号。在样例中, 表示该样例与测试点 的数据范围相同。
第二行四个整数 。
第三行一个长度为 的整数序列 。
输出格式
输出一个数,表示答案。
样例 #1
样例输入 #1
1 |
样例输出 #1
18 |
提示
【样例 1 解释】
最终序列共有 种可能:
- ,不和谐对有 ,所以该序列的不和谐度是 。
- ,不和谐对有 ,所以该序列的不和谐度是 。
- ,不和谐对有 ,所以该序列的不和谐度是 。
- ,不和谐对有 ,所以该序列的不和谐度是 。
- ,不和谐对有 ,所以该序列的不和谐度是 。
- ,不和谐对有 ,所以该序列的不和谐度是 。
答案即为 。
【样例 2】
见下发文件中的 starry/starry2.in 与 starry/starry2.ans。
该样例满足测试点 。
【样例 3】
见下发文件中的 starry/starry3.in 与 starry/starry3.ans。
该样例满足测试点 。
【样例 4】
见下发文件中的 starry/starry4.in 与 starry/starry4.ans。
该样例满足测试点 。
【样例 5】
见下发文件中的 starry/starry5.in 与 starry/starry5.ans。
该样例满足测试点 。
【样例 6】
见下发文件中的 starry/starry6.in 与 starry/starry6.ans。
该样例满足测试点 。
【数据范围】
| 测试点编号 | ||
|---|---|---|
对于全部数据,满足 ,, 。





